Truth Tables

Consider the following three formulas:

1. $\neg(P\wedge Q)$
2. $(\neg P\wedge\neg Q)$
3. $(\neg P\vee \neg Q)$

These formulas have different syntax trees:

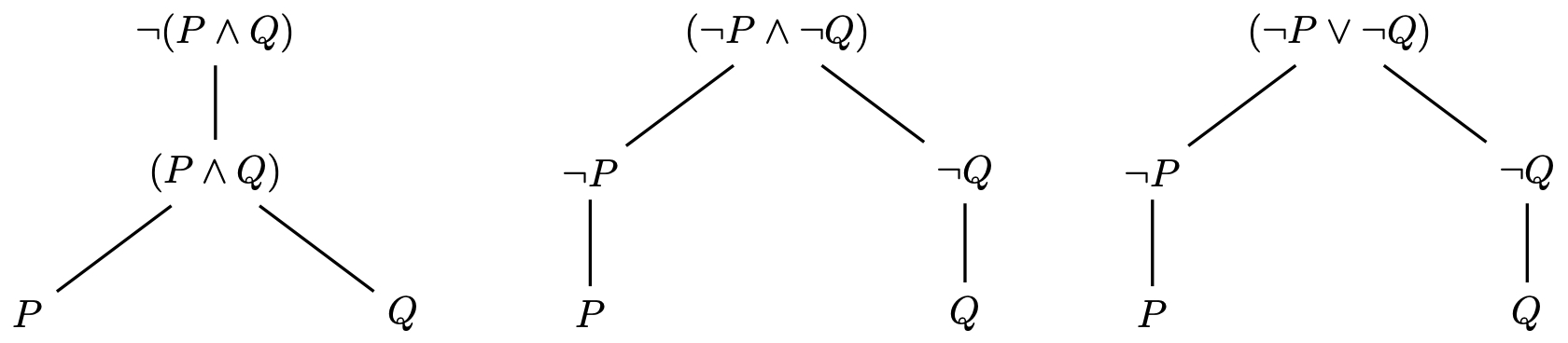
There is something more that we can say about the formulas: two of the above formulas always have the same truth value. See if you can figure out which two formulas always have the same truth value before reading further.

Each atomic proposition can be assigned any of the two possible truth values, so there are two possible truth value functions for a single atomic proposition. For two atomic propositions, there 4 possible truth value functions. For instance, there are 4 ways to assign truth values to the atomic propositions $P$ and $Q$. It is common to list the different truth value functions in a table, where each atomic proposition labels a column and each row is an assignment of truth values to the formulas in the columns:

	$P$	$Q$
1.	$\mathsf{T}$	$\mathsf{T}$
2.	$\mathsf{T}$	$\mathsf{F}$
3.	$\mathsf{F}$	$\mathsf{T}$
4.	$\mathsf{F}$	$\mathsf{F}$

For example, row 2 is the truth value assignment that assigns $\mathsf{T}$ to $P$ and $\mathsf{F}$ to $Q$. Each additional atomic proposition doubles the number of rows. For example, there are 8 truth value functions for the atomic propositions $P$, $Q$ and $R$:

$P$	$Q$	$R$
$\mathsf{T}$	$\mathsf{T}$	$\mathsf{T}$
$\mathsf{T}$	$\mathsf{T}$	$\mathsf{F}$
$\mathsf{T}$	$\mathsf{F}$	$\mathsf{T}$
$\mathsf{T}$	$\mathsf{F}$	$\mathsf{F}$
$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$
$\mathsf{F}$	$\mathsf{T}$	$\mathsf{F}$
$\mathsf{F}$	$\mathsf{F}$	$\mathsf{T}$
$\mathsf{F}$	$\mathsf{F}$	$\mathsf{F}$

More generally, we have the following:

Observation. If there are $n$ atomic propositions, then there are $2^n$ different truth value functions.

Method to find all truth values for formulas: Suppose that we are interested in all the possible truth values of one or more formulas. Below are the steps to find all the possible truth values for a collection of formulas:

1. Write down all the atomic propositions that appear in the formulas.
2. Create a truth table listing all the truth value functions for the atomic propositions identified in step 1.
3. Add columns for each formula. You may want to add columns for some of the subformulas to make the calculations easier.
4. Using the rules for assigning truth values to complex formulas (i.e., by chasing truth up the syntax tree), write a truth value for each formula in each row of the truth table.

Example

The truth values for the 3 formulas from the beginning of this section ($\neg(P\wedge Q)$, $(\neg P\vee\neg Q)$, and $(\neg P\wedge \neg Q)$) are given in the following table:

$P$	$Q$	$\neg (P\wedge Q)$	$(\neg P\vee \neg Q)$	$(\neg P\wedge \neg Q)$
$\mathsf{T}$	$\mathsf{T}$	$\mathsf{F}$	$\mathsf{F}$	$\mathsf{F}$
$\mathsf{T}$	$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{F}$
$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{F}$
$\mathsf{F}$	$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{T}$

Note that $\neg(P\wedge Q)$ and $(\neg P\vee\neg Q)$ always have the same truth value, but this is not true for any other pair of formulas.

Practice Questions

1. Find all possible truth values for $(P\rightarrow \neg Q)$

2. Find all possible truth values for $(P\rightarrow Q)\vee (Q\rightarrow P)$

3. Find all possible truth values for $(P\wedge \neg (Q\vee \neg R))$

4. Find all possible truth values for $(\neg (P\vee Q)\wedge P)$

5. Find all possible truth values for $\neg\neg (P \vee Q)$

6. Find all possible truth values for the formulas $P\rightarrow Q$, $\neg Q$ and $\neg P$

7. Find all possible truth values for the formulas $P\wedge Q$ and $\neg P\vee R$

8. Find all possible truth values for $(P\wedge \neg P)\rightarrow Q$

9. Find all possible truth values for the formulas $P\rightarrow Q$, $P\wedge\neg Q$, and $\neg P\vee Q$

10. Find all possible truth values for $(P\rightarrow (Q\rightarrow P))$

11. Find all possible truth values for $(P\leftrightarrow (Q\wedge R))$

12. Find all possible truth values for $(\neg (P\vee Q)\leftrightarrow P)$

13. Find all possible truth values for $P\leftrightarrow \neg P$

14. Find all possible truth values for $(P\leftrightarrow Q)$ and $(P\wedge Q)$

15. Find all possible truth values for $(P\leftrightarrow \neg Q)$ and $(\neg Q\rightarrow P)$

16. Find all possible truth values for $(P\rightarrow Q)$, $(\neg P\vee Q)$, and $\neg (P\wedge \neg Q)$.

17. Find all possible truth values for $(P\wedge Q)$, $(\neg P\vee \neg Q)$, and $(P\rightarrow R)$.

18. Find all possible truth values for $(P \leftrightarrow (P\wedge Q))$.

19. Find all possible truth values for $(P \rightarrow Q)$ and $((P\wedge R) \rightarrow Q)$.

20. Find all possible truth values for $(P \rightarrow Q)$, $(Q \rightarrow P)$, and $(P\leftrightarrow Q)$.