Validity

Consider a truth table for the formulas $P\vee Q$, $\neg P$ and $\neg Q$.

	$P$	$Q$	$(P\vee Q)$	$\neg P$	$\neg Q$
1.	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{F}$	$\mathsf{F}$
2.	$\mathsf{T}$	$\mathsf{F}$	$\mathsf{T}$	$\mathsf{F}$	$\mathsf{T}$
3.	$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{F}$
4.	$\mathsf{F}$	$\mathsf{F}$	$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$

A couple observations about this truth table:

• Each pair of formulas are satisfiable: $P\vee Q$ and $\neg P$ are both true in row 3; $P\vee Q$ and $\neg Q$ are both true in row 2; and $\neg P$ and $\neg Q$ are both true in row 4.
• There is no row in which all three formulas are true: The only row in which $P\vee Q$ and $\neg P$ are true is row 3, but $\neg Q$ is false in this row. When this happens, we say that the set of formulas $\{P\vee Q, \neg P, \neg Q\}$ is not satisfiable.
• In every row in which $P\vee Q$ and $\neg P$ are true, $Q$ is true: The only row in which $P\vee Q$ and $\neg P$ are true is row 3, and in this row $Q$ is true.
• In every row in which $Q$ is false, at least one of $P\vee Q$ or $\neg P$ is false. The two rows in which $Q$ is false is 2 and 4. In row 2, $\neg P$ is false and in row 4 $P\vee Q$ is false.

The last two observations explain why the argument with premises $P\vee Q$ and $\neg P$ and conclusion $Q$ is valid.

Recall (see the section on argument form) that we denote an inference, or argument, by listing the premises separated a comma followed by '$\Rightarrow$' followed by the conclusion. For instance, the argument with premises $P\vee Q$ and $\neg P$ and conclusion $Q$ is written as:

$$P\vee Q, \neg P \Rightarrow Q.$$

The truth table given above shows that this argument is valid, where validity of an argument is defined as follows.

Validity

An argument, or inference, $X_1, \ldots, X_n\Rightarrow Y$ is valid if there is no truth value assignment that makes each $X_1, \ldots, X_n$ true and $Y$ false.

We write $X_1, \ldots, X_n\models Y$ when $X_1, \ldots, X_n\Rightarrow Y$ is valid.

We write $X_1, \ldots, X_n\not\models Y$ when $X_1, \ldots, X_n\Rightarrow Y$ is not valid.

Example

$P, P\rightarrow Q \models Q$: That is, $P, P\rightarrow Q \Rightarrow Q$ is valid. To see this, we first construct a truth table with a column for $P\rightarrow Q$:

	$P$	$Q$	$(P\rightarrow Q)$
1.	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{T}$
2.	$\mathsf{T}$	$\mathsf{F}$	$\mathsf{F}$
3.	$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$
4.	$\mathsf{F}$	$\mathsf{F}$	$\mathsf{T}$

The second step is to verify that there is no truth value assignment that makes each of $P$ and $P\rightarrow Q$ true and $Q$ false. Recall that each row of the truth table is a truth value assignment, and the above truth table lists all the relevant truth value assignments to determine the validity of the argument. We can explain why the argument is valid in two ways:

• Row 1 is the only row in which $P$ and $P\rightarrow Q$ is true, and in that row $Q$ is true. This means that there is no row in which $P$ and $P\rightarrow Q$ are both true and $Q$ is false. So, the argument $P, P\rightarrow Q\Rightarrow Q$ is valid.

• $Q$ is false in rows 2 and 4. In row 2, $P\rightarrow Q$ is false, and in row 4, $P$ is false. This means that every row in which $Q$ is false, at least one of the premises is false. That is, there is no row in which $P$ and $P\rightarrow Q$ are both true and $Q$ is false. So, the argument $P, P\rightarrow Q\Rightarrow Q$ is valid.

Example

$Q, P\rightarrow Q \not\models P$: That is, $Q, P\rightarrow Q \Rightarrow P$ is not valid. To see this, we first construct a truth table with a column for $P\rightarrow Q$:

	$P$	$Q$	$(P\rightarrow Q)$
1.	$\mathsf{T}$	$\mathsf{T}$	$\mathsf{T}$
2.	$\mathsf{T}$	$\mathsf{F}$	$\mathsf{F}$
3.	$\mathsf{F}$	$\mathsf{T}$	$\mathsf{T}$
4.	$\mathsf{F}$	$\mathsf{F}$	$\mathsf{T}$

The second step is to verify that there is a truth value assignment that makes $Q$ and $P\rightarrow Q$ both true and $P$ false. In row 3, $Q$ and $P\rightarrow Q$ is true and $P$ is false. This means that there is a truth value assignment that makes $Q$ and $P\rightarrow Q$ both true and $P$ false. This means that the argument $Q, P\rightarrow Q\Rightarrow P$ is not valid.

The following picture summarizes the procedure to determine whether an argument $X_1, X_2, \ldots, X_n\Rightarrow Y$ is valid.

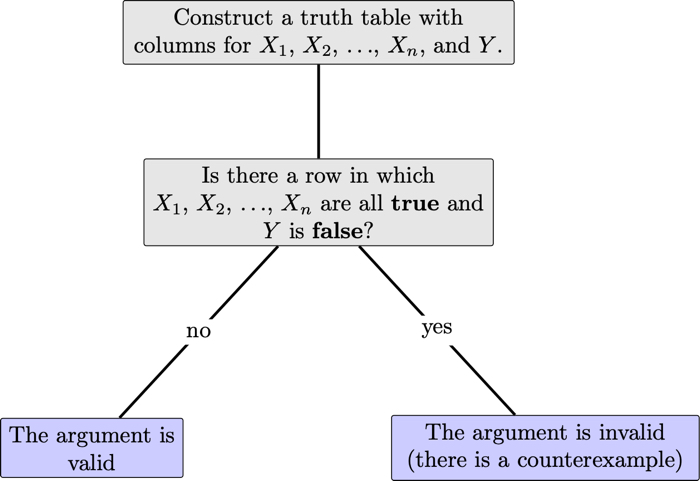
The following are equivalent ways to define validity of an argument:

• There is no truth value assignment that makes all the premises true and the conclusion false.
• Every truth value assignment that makes all the premises true also makes the conclusion true.
• Every truth value assignment that makes the conclusion false also makes at least one of the premises false.

Practice Questions

I. Answer the following true/false questions.

1. True or False: If an argument has a false conclusion, then it is invalid.
   True False

   ​

   The conclusion of a valid argument can be false as long as at least one of the premises of the argument is also false.

2. True or False: If the conclusion of a valid argument is false, then at least one of its premises is false.

   TrueFalse

   ​

   If there is a row in a truth table for the argument in which the conclusion is false, then at least one premise must also be false (otherwise, the row would be a counterexample showing that the argument is not valid).

3. True or False: Adding a premise to a valid argument may make the argument invalid.

   TrueFalse

   ​

   Suppose that $X\models Z$. This means that every row of a truth table that makes $X$ true, also makes $Z$ true. To see that $X,Y\models Z$, consider any row that makes both $X$ and $Y$ true. Since $X\models Z$ and the row makes $X$ true, that row must also make $Z$ true. So, $X,Y\models Z$.

4. True or False: If an argument has a contradiction as a premise, then the argument is valid.

   TrueFalse

   ​

   If a premise is a contradiction, then there is no truth value assignment that makes that premise true. This means that there is no truth value assignment that makes all the premises true and the conclusion false. So, the argument is valid.

5. True or False: If an argument has a tautology as a conclusion, then the argument is valid.

   TrueFalse

   ​

   The conclusion is a tautology, then every truth value assignment makes the conclusion true. This means that there is no truth value assignment that makes all the premises true and the conclusion false. So, the argument is valid.

6. True or False: If there is some truth value assignment that makes all the premises and the conclusion are true, then the argument is valid.

   TrueFalse

   ​

   An argument is valid if every truth value assignment that makes all the premises true also makes the conclusion true.

7. True or False: If an argument has premises that are not satisfiable, then the argument is valid.

   TrueFalse

   ​

   If there are premises of an argument that are not satisfiable, then there is no truth value assignment that makes all the premises true. This means that there is no truth value assignment that makes all the premises true and the conclusion false. So, the argument is valid.

II. Use a truth table to determine whether the argument is valid.

1. $P\rightarrow Q, \neg Q \Rightarrow \neg P$

2. $\neg P\rightarrow Q, \neg Q \Rightarrow P$

3. $P\rightarrow Q, Q \Rightarrow P$

4. $P\rightarrow Q, Q \rightarrow R \Rightarrow (P \vee Q) \rightarrow R$

5. $P\rightarrow Q, P\rightarrow R \Rightarrow P\rightarrow (Q \wedge R)$

6. $P\rightarrow Q, P \Rightarrow Q$

7. $P\rightarrow Q, P, \neg R \Rightarrow Q$

8. $P\rightarrow Q, P, \neg Q \Rightarrow Q$

9. $P\wedge Q\rightarrow R, P\vee Q \Rightarrow R$

10. $P\wedge Q\rightarrow R, P \Rightarrow Q\rightarrow R$

11. $P \vee Q, Q\rightarrow R \Rightarrow P\wedge R$

12. $(P\rightarrow (Q\rightarrow R)), (Q\wedge R) \Rightarrow \neg\neg P$

13. $((P\wedge Q)\vee (P\rightarrow \neg Q)), (Q\rightarrow R) \Rightarrow (\neg R\rightarrow P)$

14. $(\neg (P \vee Q) \rightarrow P), (P\wedge Q) \Rightarrow P$

15. $\neg (P \vee Q) \rightarrow P, \neg P, Q \Rightarrow R$